Graph Pyramid Solution of Travelling Salesman Problem
Introduction

Traveling salesperson problem (TSP) is a combinatorial optimization task of finding the shortest tour of n cities given the intercity costs. When the costs between cities are Euclidean distances, the problem is called Euclidean TSP (E-TSP). TSP as well as E-TSP belongs to the class of difficult optimization problems called NP-hard and NP-complete if posed as a decision problem [1]. The straightforward approach by using brute force search would be using all possible permutations for finding the shortest tour. It is impractical for large n since the number of permutations is (n-1)!/2.

Because of the computational intractability of TSP, researchers concentrated their efforts on finding approximating algorithms. Good approximating algorithms can produce solutions that are only a few percent longer than an optimal solution and the time of solving the problem is a low-order polynomial function of the number of cities [2, 3, 4]. The last few percent to reach optimality are computationally the most expensive to achieve.

It is by now well established that humans produce close-to-optimal solutions to E-TSP problems in time that is (on average) proportional to the number of cities [5, 6, 7]. This level of performance can not be reproduced by any of the standard approximating algorithms. Some approximating algorithms produce smaller errors but the time complexity is substantially higher than linear, other algorithms are relatively fast but produce substantially higher errors. It is therefore of interest to identify the computational mechanism used by the human brain.

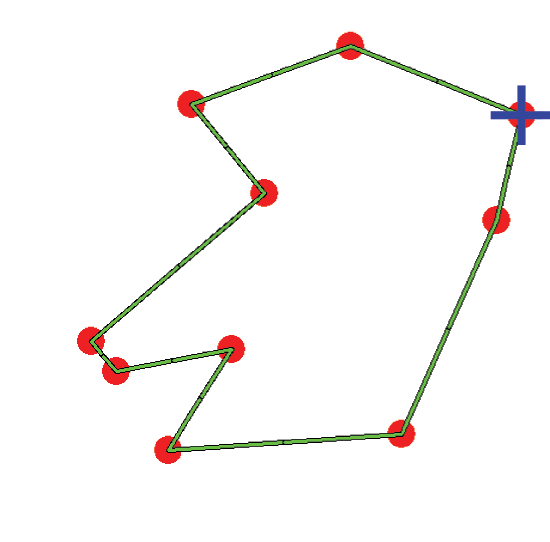
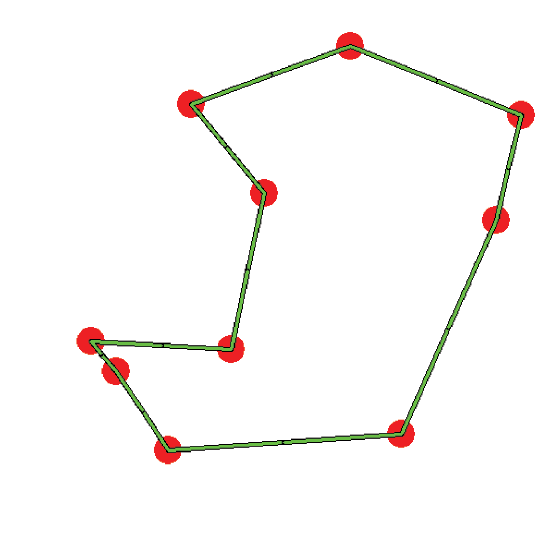
A simple way to present E-TSP to a subject is to show n cities as points on a computer screen and ask the subject to produce a tour by clicking on the points. In the Figure 1 (a), an E-TSP example of 10 cities is shown; in (b) the solution given by a human, and in (c) by the optimal solver. The tours produced by the subjects are, on average, only a few percent longer than the shortest tours (in the Figure 1 (b) the cross depicts the starting position and the arrow the orientation used by the subject). The solution time is a linear function of the number of cities [5, 6]. Two attempts to emulate human performance by a computational model were undertaken in [5, 6]. In [5], authors attempt to formulate a new approximating algorithm for E-TSP motivated by the failure to identify an existing algorithm that could provide a good fit to the subjects' data. The main aspects of the models in [5, 7, 13] are its

1. (multiresolution) pyramid architecture, and
2. a coarse to fine process of successive tour approximations.

---

Figure 1. E-TSP and solutions given by human (b) and optimal solver (c)

(a)	(b)	(c)
10 city problem

---

They showed that performance of this model (proportion of optimal solutions and average solution error) is statistically equivalent to human performance. Pyramid algorithms have been used extensively in both computer and human vision literature (e.g. [8]), but not in problem solving. The work of [5, 9] was the first attempt to use pyramid algorithms to solve the E-TSP. One of the most attractive aspects of pyramid algorithms, which make them suitable for problems such as early vision or E-TSP, is that they allow to solve (approximately) global optimization tasks without performing a global search. A similar pyramid algorithm for producing approximate E-TSP solutions with emphasis on trade-off between computational complexity (speed) and error in the solution (accuracy) and not on modeling human performance is formulated in [4, Chapter 5], and [10].↑

Approximating TSP by MST based Graph Pyramid
The Model

In the graph pyramid framework, the TSP input is represented by graphs where cities are represented by vertices, and the intercity neighborhoods by edges. Each vertex of the constructed input graph must have at least two edges for the TSP tour to exist. A level (k) of the graph pyramid consists of a graph G_k. Moreover the graph is attributed, G=(C,N,w_v,w_e), where w_e:N→ R⁺ is a weighted function defined on edges N. The weights w_e are Euclidean distances in the E-TSP and w_v:C → R⁺ is a weighted function defined on cities C. I.e. each vertex (city) has as a weight its position in the Cartesian coordinate system. Finally, the sequence G_k, 0 < k < h is called irregular graph pyramid.

Let G₀=(C,N,w_v,w_e) be the input graph, with weights on edges given as distances in L₂ space. The goal of the TSP is to find an nonempty ordered sequence of vertices and edges (v₀,e₁,v₁,...,v_k-1,e_k,v_k,...,v₀) over all vertices of G₀ such that all the edges and vertices are distinct, except the start and the end vertex v₀. This tour is called the optimal tour t_opt and the sum of edge weights in this tour is minimal, i.e.

topt = ∑ e∈ t  we→ min ,

where w_e is the weight of edge e.

We use local to global and global to local processes in the graph pyramid to find a good solution t^*, approximating the E-TSP. The main idea is to use:

• bottom-up processes to reduce the size of the input, and
• top-down refinement to find an (approximate) solution.

The size of the input (number of vertices in the graph) is reduced such that an optimal (trivial) solution can be found by the combinatorial search, e.g. for a 3 city instance (not all cities are co-linear) there is only one solution, not needing any search, and this is the optimal one. For a 4 city input (not all co-linear) there are three solutions from which two are non-optimal since they cross edges. A pyramid is used to reduce the size of the input in the bottom-up process. The (trivial) solution is then found at the top of the pyramid and refined in a process emulating fovea by humans using lower levels of this pyramid, i.e. the vertical neighborhoods (parent-children relations) are used in this process to refine the tour. The final, in general non-optimal, solution is found when all the cities at the base level of the pyramid are in the tour. The steps needed to find the E-TSP solution are shown below.

---

Approximating E-TSP Solution by an MST Graph Pyramid
Input: Attributed graph G₀=(C,N,w_v,w_e), and parameters r and s

1. partition the input space by preserving approximate location:
   create graph G₀
2. reduce number of cities bottom-up until the graph contains s vertices:
   build graph pyramid G_k, k=0,...,h, where s=|G_h|, and such that a father can have maximum of r childrens
3. find the optimal tour t_a for the graph G_h
4. refine solution top-down until all vertices at the base level are processed:
   refine t_a until level 0 is reached

Output: Approximate TSP solution t^*.

---

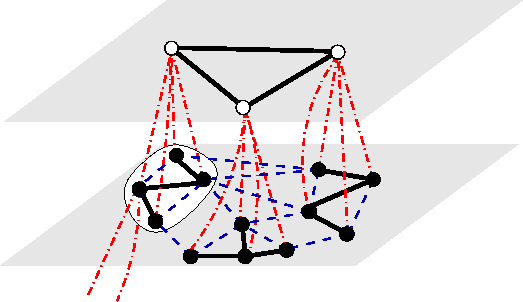
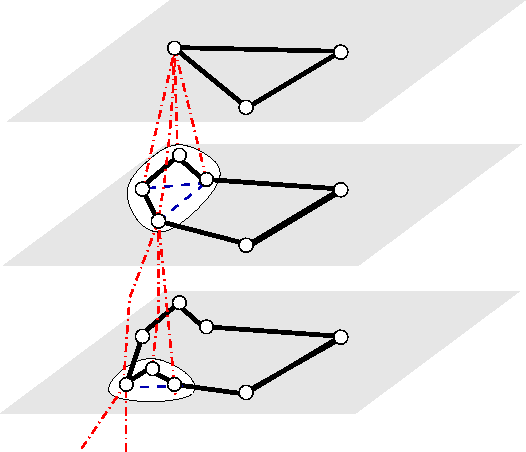
The main idea in step (b) is that cities being close neighbors are put into a cluster and considered as a single city at reduced resolution. By doing this recursively one produces a pyramid representation of the problem. It is well known that the human visual system represent images on multiple level of scales and resolution [11,12]. In Figure 2. this step is illustrated for two levels of the pyramid.

---

Figure 2. Building the graph pyramid and finding the first TSP tour approximation.

(a) Bottom-up reduction of resolution ⇑	(b) Initial tour ta
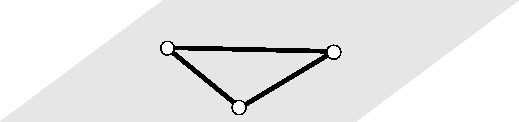r=4 and s=3

---

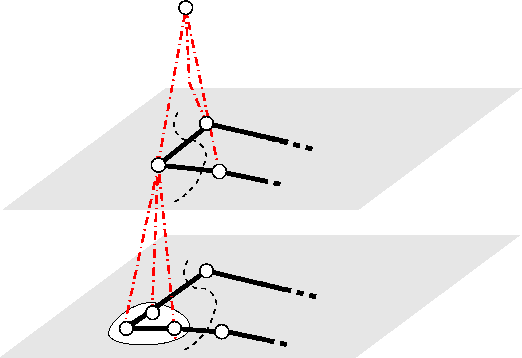
The main idea in step (d) is using the tour t_a found at level h of the graph pyramid as the first approximation of the TSP tour t^*. This tour is then refined using the pyramid structure already built. The refinement process starts by choosing (randomly) a vertex v in the tour t_a. Using the parent-child relationship, this vertex is expanded into the subgraph G'_h-1. In this subgraph a path between vertices (children) is found that makes the overall path t'_a the shortest one (see Figure 3. a). Since the number of children from a father in G'_h cannot be larger than r, a complete search is a plausible approach to find the path with the smallest contribution in the overall length of the tour t'_a.

---

Figure 3. Building the graph pyramid and finding the first TSP tour approximation.

(a) Top-down refinement of ta in t'a ⇓	(b) The flow of processing ⇓

---

For more details consult reference [14].↑

References ↑

Pyramid Solution of Travelling Salesman Problem (TSP)

This tool allows to solve the Traveling Salesman problem in a coarse to fine strategy.

References Tool to work with

• Source code (April, 25 2007 - Andreas Lehrbaum)

Usage notice

↑

MST Pyramid Solution of Travelling Salesman Problem - Demo

Graph Pyramid Model

Introduction

Graph Pyramid Solution

References

TSP Source Code

TSP Demostration

←