Foveating Pyramid Solution of Travelling Salesman Problem
Introduction

In this short intoroduction we discuss the mental mechanisms involved in solving the Traveling Salesman Problem (TSP). TSP refers to the task of finding the shortest tour of n cities given the intercity distances (costs). When the distances between cities are Euclidean, the problem is called E-TSP [4]. A simple way to present E-TSP to a subject is to show n points on a computer screen and ask the subject to produce a tour by clicking on the points. TSP (including E-TSP) belongs to the class of difficult problems called NP-hard. Difficult means that finding an optimal solution (i.e., the shortest tour) may require, in the worst case, performing an exhaustive search through all tours. Because the number of tours for an n-city problem is equal to (n-1)!/2 and, thus, grows very quickly with the number of cities n, determining lengths of all tours is usually impossible. For this reason, TSP is called computationally intractable. Because of the intractability of TSP, researchers interested in problem solving concentrated their efforts on finding approximating algorithms - that is, algorithms that can produce nearoptimal solutions fairly quickly. Good approximating algorithms can produce solutions that are only a few percent longer than an optimal solution, and the time of solving the problem is a low-order polynomial function of the number of cities [1, 2, 3].

Interestingly, humans are known to produce close-to-optimal solutions to E-TSP problems in time that is (on average) proportional to the number of cities [4, 5, 6, 7]. That is, the tours produced by the subjects are, on average, only a few percent longer than the shortest tours, and the solution time is a linear function of the number of cities. The two main attempts to emulate human performance by a computational model were undertaken by Graham et al. [4] and by MacGregor et al. [5]. The present study directly derives from that of Graham et al. model [4]. In particular, the model presented in this paper is an elaboration of that of Graham et al.

Graham's et al. attempt to formulate a new approximating algorithm for E-TSP was motivated by the failure to identify an existing algorithm that could provide a good fit to the subjects' data. The main aspect of Graham et al.'s model [4] was its

1. (multiresolution) pyramid architecture, and
2. coarse-to-fine process of successive tour approximations.

They showed that performance of this model (proportion of optimal solutions and average solution error) is statistically equivalent to human performance. Pyramid algorithms have been used extensively in both computer and human vision literature (e.g., Jolion and Rosenfeld [8], Pizlo et al. [9]) but not in problem solving. The work of Graham et al. was the first attempt to use pyramid algorithms to solve TSP [9, 10]. One of the most attractive aspects of pyramid algorithms, which makes them suitable for problems such as early vision or E-TSP, is that they allow the solving (approximately) of global optimization tasks without performing a global search. Shortly after Graham et al. formulated their model, Arora described a pyramid algorithm for producing approximate E-TSP solutions [11]. Arora was not interested in modeling human performance but, rather, in formulating an algorithm that allows for trading computational complexity (speed) for error of the solution (accuracy; see also [3], for a description of Arora's results).

Approximating TSP by Foveating Pyramid
The Model

The pyramid that simulates nonuniform distribution of visual aquity is called foveating pyramid (FP). In the human visual system, the visual acuity is inversely proportional to the distance from the center of the retina, fovea [12]. This dependence of visual acuity on the distance from the fovea is related to the nonuniform density of receptors on the retina. The nonuniform density of receptors allows the visual system to avoid handling too much visual information at one time but to still have a high resolution within the fovea and a quite large field of view in the periphery. The foveating pyramid model has similar properties. It is a conventional pyramid in the sense of having multiple representations of the image, the representations being different in the sizes of the receptive fields and their resolution. Unlike conventional pyramids, where every layer has information about the entire image, in the new pyramid the highest resolution representation (at the first layer) has information about only a small part of the image around its fixation point. The representation on the second layer has information about a larger part of the image, but the information is characterized by a lower resolution than the first layer and so on.

When a human subject produces a solution to an E-TSP problem by working successively on individual parts of the problem, the size of the attentional window is not necessarily fixed. It is known that a human observer may attend to a small part of the visual field when the details are important. Alternatively, she may attend to a large part of the visual field when the global aspects are of interest [13]. This pyramid model has similar properties. The choice about which part of the E-TSP problem to analyze and how large this part should be is established in a top-down process in which the global aspects are used to guide decisions on more local representations.

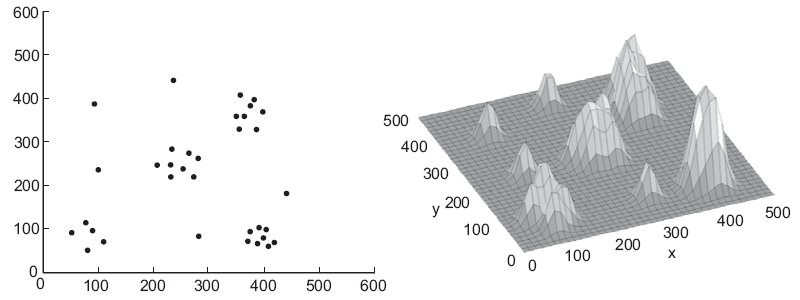
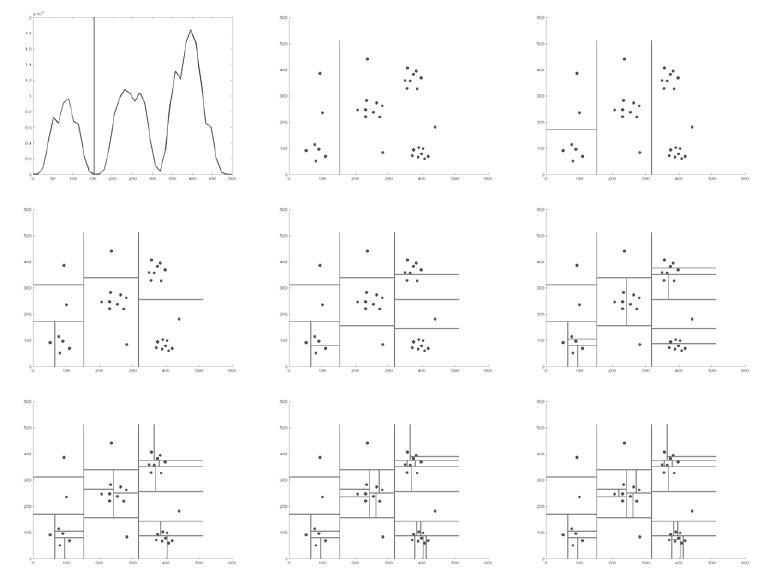
Before the solution process begins, the FP forms a hierarchical representation of the problem. The goal of building this representation is to identify clusters of cities on many levels of resolution, as well as to establish spatial relations among the clusters. This is done in a top-down process called bisection, which is illustrated in Figure 1. Figure 1a shows an E-TSP problem where several clearly defined clusters are present. Figure 1b shows the intensity distribution after the problem was blurred by a Gaussian filter (the size of the Gaussian filter is not critical). Then, for each position on the X-axis, the maximum intensity I_maxY(X) along the Y direction is found. Similarly, for each position on the Y-axis, the maximum intensity I_maxX(Y) along the X direction is found. Then, a minimum of each of these two distributions is determined, min I_maxY(X), min I_maxX(Y), and the smaller of the two corresponds to the boundary between two clusters on the coarsest level (see Figure 1b, top left and top center panels). Then, the process of blurring (with proportionally smaller filters) and bisecting is repeated as shown on the remaining panels of Figure 1b. The bisection process ends when each city is in its own cluster. After the pyramid representation is built, the solution process begins.

The solution process starts at the top layer, h, in which the entire problem is represented by two clusters. The initial tour involves just these two clusters. More exactly, the tour involves centers of gravity of the cities within clusters. The starting city is chosen randomly. Then, the tour is refined recursively within the receptive fields that contain the starting city. As a result, the tour is represented on many layers of the pyramid; different parts of the tour "residing" on layers having different spatial resolution. The cities in the fovea are represented with the highest resolution, and the cities that are farther away from the fovea are represented with resolution that falls off gradually. After the starting city and its immediate neighborhood is described at the highest resolution, the simulated fovea is moved to the next city (clockwise or counterclockwise) on the existing tour, and the part of the tour "ahead" of the current city is projected down to layers with higher resolution so that a gradual transition between resolutions is maintained (the direction of the solution, clockwise vs. counterclockwise, is determined randomly). When a part of the tour on a layer j is projected to layer j-1, new clusters emerge. These clusters are inserted into the existing tour by using cheapest insertion [2]. Specifically, the new cluster (which is treated as a city) is inserted between pairs of consecutive cities in the existing tour, but only those pairs that are within k cities of the current city in the existing tour are tried. Thus, the parameter k represents the magnitude of local search involved in solving TSP. The values of k in the range between 0 and 8 were used. Larger values of k correspond to greater amounts of local search, which is likely to lead to better solutions.

---

Figure 1. (a) On the left is a 34-city problem with four clusters. On the right is an intensity distribution produced by Gaussian blurring. (b) The top-down (coarse-to-fine) process of determining cluster boundaries.

(a) (click on the image for better resolution)

(b) (click on the image for better resolution)

---

---

For more details consult references [14].↑

References ↑

Fovea Pyramid Solution of Travelling Salesman Problem (TSP)

This tool allows to solve the Traveling Salesman problem in a coarse to fine strategy.

References Tool to work with

• Demo version of the TSP (1.95.2)(June, 10 2004 - Jack Saalweachter and Emil Stefanov)

Usage notice

↑

MST Pyramid Solution of Travelling Salesman Problem - Demo

Start the small demo to see the solution process.

Usage notice

↑

Foveating Pyramid Model

Introduction

Foveating Pyramid Solution

References

TSP Application

TSP Demostration

←