|
1990 Pattern Recognition and Image Processing Group 2021 2021- Virtual & Augmented Reality |

|
Gray Level Pyramids
In this demonstration we give a short introduction to gray level pyramids. Each section of this demonstration is splitted in an introduction, in which we give an overview about the kind of the demonstrated pyramid, followed by demonstrations. We introduce:
Regular Pyramids
There are two terms to describe the structure of a regular pyramid:
- the reduction factor, which determines the rate by which the number of cells decrease from level to level, and
- the reduction window, which associates a set of cells of the level directly below to every (higher level) cell. It covers the area of its associated cell. Reduction windows are mostly rectangular shaped.
Formally, the structure of a regular pyramid will be described by (number of colums) x (number of rows) / (reduction factor).
A pyramid is defined by its structure and its operation, which is responsible for the bottom-up information flow within the pyramid. This operation is called the reduction function.
In gray level pyramids, the contents of cells are gray values or color vectors. Every level of the pyramid is a picture. Different reduction functions can be used to fill the bottom-up cells of the pyramid.
Regular Pyramid Example
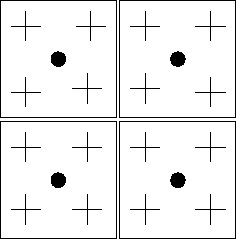
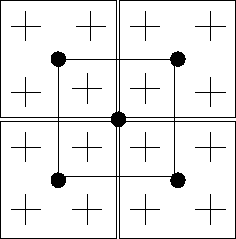
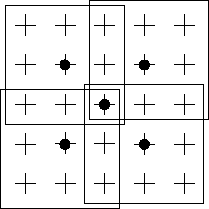
The next structures are common types of pyramids. A (+) indicates pixels in level k, a (.) indicates a pixel of level k+1 and a rectangle shows the reduction window of a pyramid.
| Classical 2 x 2/4 pyramid | 2 x 2/2 pyramid | 3 x 3/2 pyramid |
 |
 |
 |
Gaussian Pyramids
Linear filters are used to remove certain unwanted effects (e.g. noise) from images while enhancing others. One way to filter an image is to convolve it with a spatial filter kernel that has the characteristics of the filter. In the continous image space, both the image I:ℝ2→ℝ and the filter kernel F:ℝ2→ℝ are continous functions, the convolution I*F is defined as:
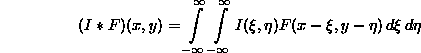
One of the famous kernels is the Gaussian filter kernel, which has some unique properties with respect to multiresolution representation.
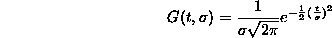
(1-dimensional case)
Using the 2-dimensional Gaussian filter kernel we get:
- G(σ)*(G(σ)*I)=G(σ√2),where G(σ√2) is called the equivalent weighting function.
- The mean μ(G(σ)*I)≈μ(I) remains the same except for deviations caused by the boundary.
The different levels of a pyramid can be built in two ways:
- iteratively level by level from the bottom to the top, or
- directly from the base using the equivalent weighting function.
Gaussian Pyramid Example
In this section we show the eight steps on building a gaussian pyramid over a 256 x 256 image. The original image shows the head of a mandril. The color image will be reduced step by step using a 5 x 5/4 gaussian pyramid. To reduce the color image we used the 3 color channels (red, green and blue) and interpreted each of them as a gray level image.

Maximum/Minimum Pyramids
Besides linear filters also other non-linear reduction functions have been used. To detect bright/dark spots in images we can use bottom-up reduction functions like maximum/minimum and average functions in a 2 x 2/4 pyramid structure.
The bright/dark spot is found in a top down search pass that links the apex of the pyramid to one pixel in the base.
The non-overlapping structure of their pyramid produces results that depend on the lateral position of the object region. But the width of a region, which is defined as the side length of the largest pyramidal cell completely contained in the region, will
vary by at most a factor of 2 when subjected to lateral translation within the pyramid. The average, when applied to a region of width 2j, j>0, at level k produces a region of width 2j-1at level k+1.
The maximum as reduction function produces a region of width at least 2j-1at level k+1. Averaging the first j levels and using the maximum/minimum above can detect bright/dark spots of width 2j or greater, instead of regions of
less width.
A possible extension of the pure 2 x 2/4 structure is the 4 x 4/4 overlapping pyramid which could be used within the same framework. It improves the results while the computational cost are only increased by a constant factor.
Minimum Pyramid Example
In this demonstration, we show the eight steps on building a minimum pyramid of a 256 x 256 image. The image shows the drillmask of a turntable. This image will be reduced step by step using a 2 x 2/4 minimum pyramid.
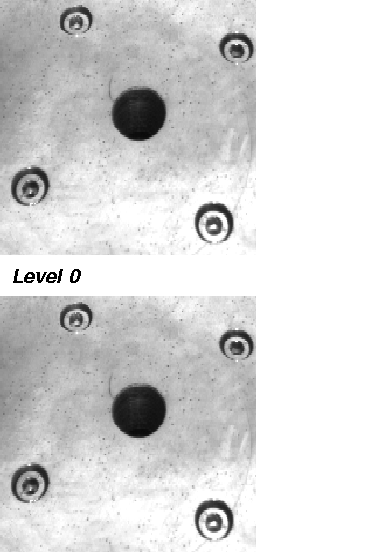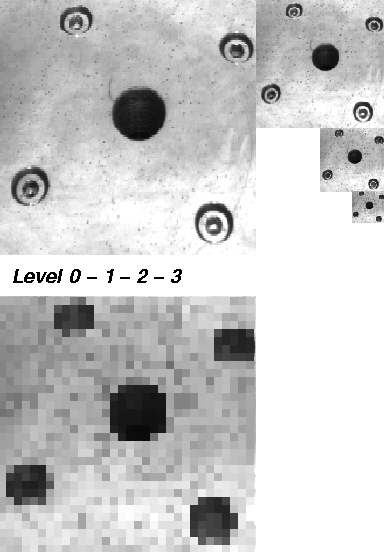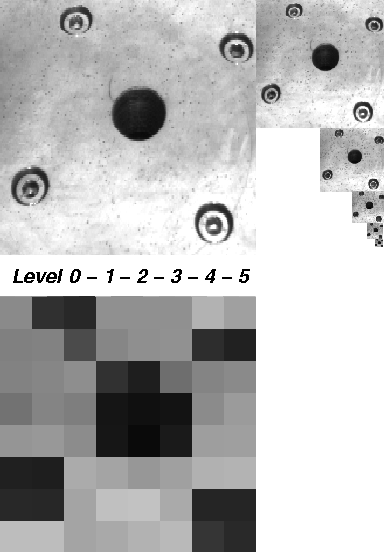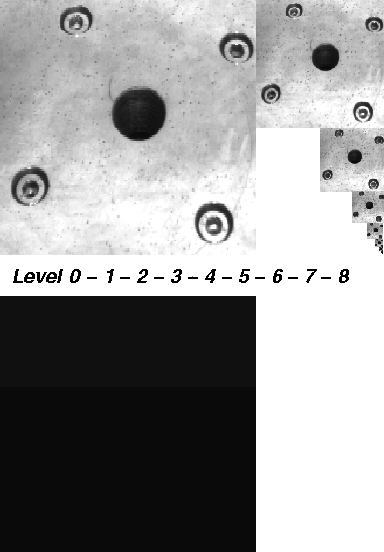
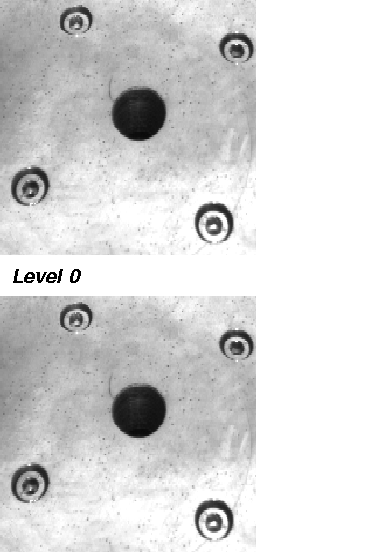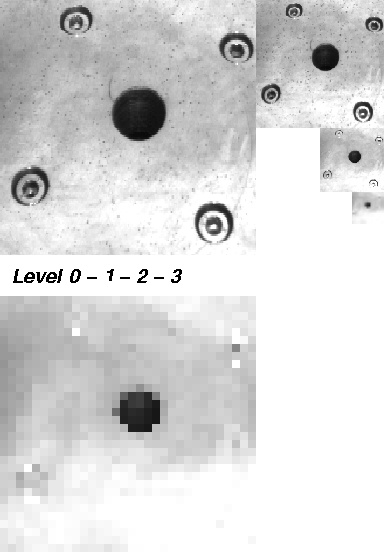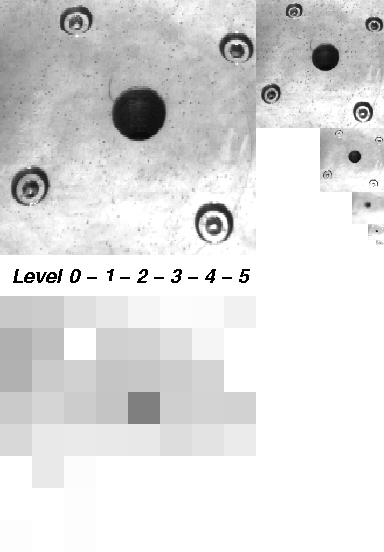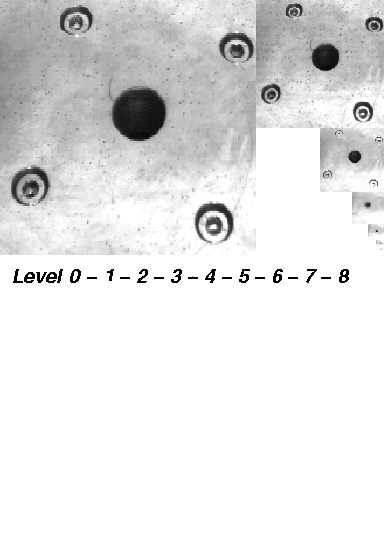
Maximum Pyramid Example
In this demonstration, we show the eight steps on building a maximum pyramid of a 256 x 256 image. The original image shows the drillmask of a turntable. This image will be reduced step by step using a 2 x 2/4 maximum pyramid.
2014-2020 PRIP, Impressum / Datenschutzerklärung
This page is maintained by Webmaster ( webmaster(at)prip.tuwien.ac.at ) and was last modified on 11. March 2015 16:35