|
1990 Pattern Recognition and Image Processing Group 2021 2021- Virtual & Augmented Reality |

|
Structure & Topology
- Graphs in Image Analysis
- Dual Graph Contraction
- Minimal Spanning Tree
- Representing Topological Structures
- Data Structures
Graphs in Image Analysis
Graph based representations are mainly used in image analysis to represent irregular structures. Graphs were used in segmentation, shape matching, video action description, technical drawings, fingerprint recognition, etc.
In the following subsections examples of graph based representations and their properties are given, followed by operations and some applications.
Representing Images by Graphs
In this demonstration we first motivate and explain the use of graphs in image analysis. In order to reduce these graphs, while preserving important structural properties, we then focus on a graph transformation called dual graph contraction. Finally, we illustrate how images are represented by graphs called minimal spanning trees and explain their applications.
About the Use of Graphs in Image Analysis
We focus on two concepts for the representation of images by graphs: a discrete one based on pixels and a continuous one based on points in a plane.
From Pixels to Graphs:
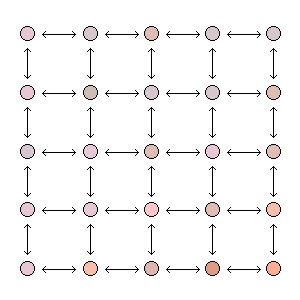
A two-dimensional digital image is usually given by a rectangular array of picture elements called pixels. This suggests the use of graphs, where each vertex represents a pixel.
| Magnify |  |
|
 |
Receptive Fields |  |
 |
Neighbourhoods |  |
| Seperate Structure and Contents | 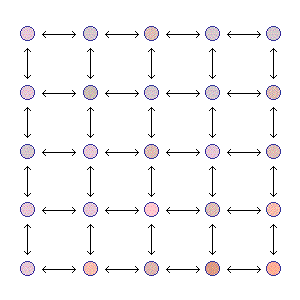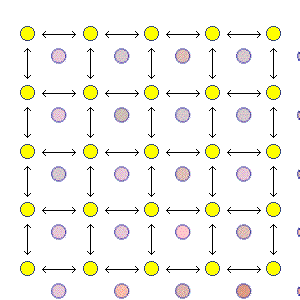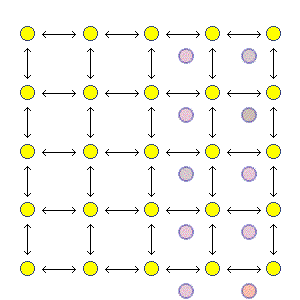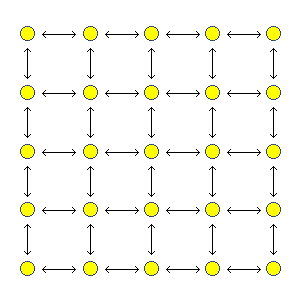 |
|
 |
Zoomout |  |
 |
Segmentation | From the pixel array... |
to the region adjacency graph (RAG)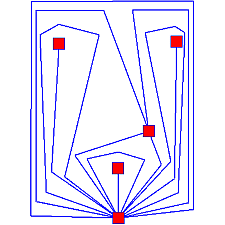 |
and the dual of the RAG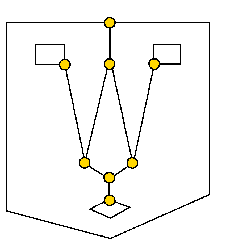 |
See W.Kropatsch and S. Ben Yacoub. A Revision of Pyramid Segmentation. In ICPR'96, Vol. 13B, pages 477-481.
Voronoi graph and Delaunay graph:
Considering points in the plane rather than pixels, the neighboring relations of the points are expressed by a plane graph called Voronoi graph. By duality it is closely related to the Delaunay graph.

Order of Construction:
- Placing red points on the plane.
- Inserting the blue edges and the blue vertices of the Voronoi graph.
- Drawing the red edges of the Delaunay graph.
Dual Graph Contraction
Dual graph contraction reduces image graphs while preserving important structural properties. The dual graph contraction animation shows the scheme of the dual graph contraction and allows the user to observe each step. Dual graph contraction is used, among other things, for connected component analysis and segmentation. Tough example images that dual graph contraction can cope with are presented.
Dual Graph Contraction Algorithm
Underneath you find the Algorithm for the Dual Graph Contraction as further discribed in PRIP-TR-42, page 2.The boxes without arrows are symbolizing states - thus clicking on them will show you the correspondig state of the graph.
The arrows are symbolizing processes - by clicking on them, you will see an animation of the transition in the direction of the arrows.
Explanation of Notation used:
- G denotes a graph.
- V denotes a set of vertices.
- E denotes a set of edges.
- The index of G, V, and E stands for the level of the pyramid.
- The dual graphs (drawn blue) are characterized by bars.
- Intermediate results are characterized by stars.
- In the contraction marked by # the non-surviving vertices are the ones with degree smaller than three.
- In the demos the brighter vertices are the surviving ones. The arrows always point towards the non-surviving vertices.
- Ni,i+1 denotes the non-surviving edges from level i to level i+1.
 |
 |
|
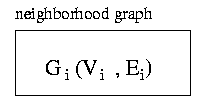 |
 |
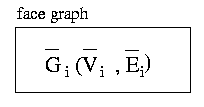 |
 |
 |
 |
 |
 |
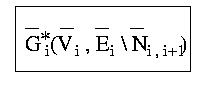 |
 |
 |
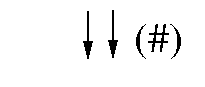 |
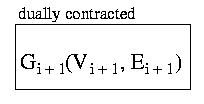 |
 |
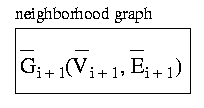 |
Example Images
| How many regions of same color are there? |  |
| Are the two X lying on the same curve? | 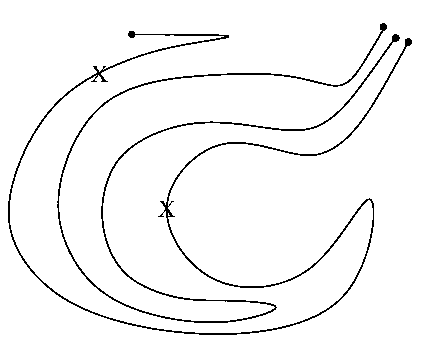 |
| How many connected components are there? |  |
Examples adapted from:
M.Bister and J.Cornelis and A. Rosenfeld. A critical view of pyramid segmentation algorithms. In Pattern Recognition Letters 1990, Vol. 11-9, pages 605-617.
P.Jolicoeur and S.Ullman and M. Mackay. A possible basic operation in the perception of spatial relations. In Memory and Cognition 1986, Vol. 14-2, pages 129-140.
P.Nacken. Image segmentation by connectivity preserving relinking in hierarchical graph structures. In Pattern Recognition 1995, Vol. 28-6, pages 907-920.
Introduction to Minimal Spanning Trees

In this demonstration we first define the minimal spanning tree (MST) and list its most important properties. We also present applications of the MST.
Definition and Properties of the Minimal Spanning Tree
Graph theoretical Definitions
- Cost of an edge of a graph: absolute distance between the gray level values of the two cells it joins.
- Spanning tree: tree that covers all vertices of a graph.
- A minimal spanning tree is a spanning tree of a graph, such that the sum of all edge costs is minimal.
Properties of the Minimal Spanning Tree
- In general, the minimal spanning tree of an image graph is not unique.
- The minimal spanning tree can be implemented for image graphs with 4- or 8-neighborhood.
- The implementation can be done using a greedy algorithm.
 |
 |
| A gray level image | and its MST |
Applications for the Minimal Spanning Tree
A major application for the minnimal spanning trees in pattern recognition is segmentation. Minimal spanning trees are used to
- find noisy pixels,
- detect and separate regions of the image,
- calculate an image pyramid based on a minimal spanning tree.
Finding noisy pixels
May the central (black) pixel below be a noisy pixel.
 |
 |
The corresponding vertex of an image pixel like that is always represented by a dead end of the minimal spanning tree. Thus endings of the minimal spanning tree with high costs to their adjacent vertices are detected as noisy pixel.
The algorithm easily leads to success on real images as shown below.
 |
 |
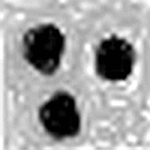
Detecting Regions
Regions with large differences in the gray level between each other are linked with a single edge of the minimal spanning tree (see below). The MST can be split up on high cost edges to receive several trees that cover the different regions.
 |
 |
 |
 |
 |
Image Pyramids based on Minimal Spanning Trees
In order to build the first level of a graph pyramid, a 4- or 8-connected image graph is constructed. Every vertex corresponds to a pixel and every edge represents a neighborhood of two pixels (A).
By choosing the minimal spanning tree as the initial graph, the result of a segmentation can be improved (B).
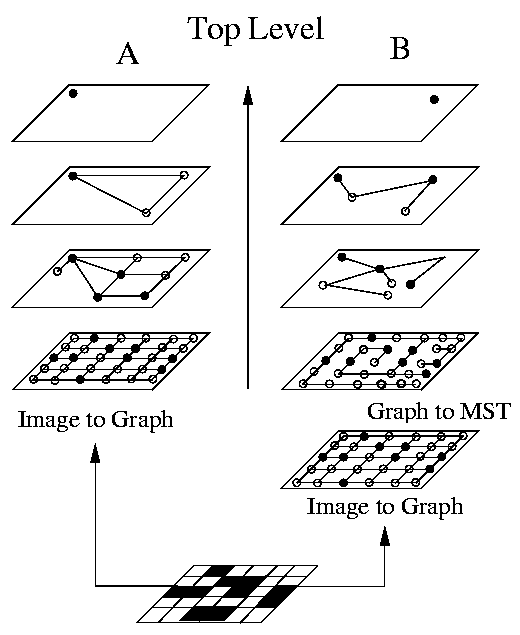
adapted from Christoph E. Mathieu and Isabelle E. Magnin, "On the Choice of the first Level on Graph Pyramids", Journal of Mathematical Imaging and Vision, Vol 6, pp 85-96, 1996.
A different approach is to build the pyramid by using the idea of the Boruvka's MST algorithm.
Representing Topological Structures
Attributed neighbourhood graphs represent an image as a graph. Attributes are derived from the colours of the pixels. Neighbourhood relations are represented by edges.
Standard and extended region adjacency graphs (RAG, RAG+) represent the adjacency relations of image regions in, for example, a segmentation. In addition to RAGs, which are simple graphs, RAG+'s keep some self loops and parallel edges to encode
inclusion relations (e.g. non-empty self-loops and parallel edges bounding non empty-faces).
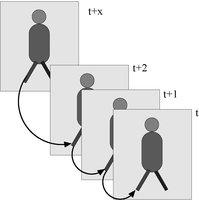
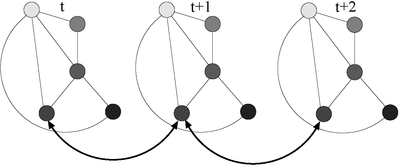
Adjacency, and more general, structure, also plays an important role in dynamic scenes i.e. processing of videos. In the TWIST project (Tracking with Structure in Computer Vision) we study the importance of structure for tracking. Structure is represented
e.g. in a graph or more generally graph pyramid representation of the segmented image and correspondence can be found by graph matching (see Figure 1).
 |
 |
| a | b |
Figure 1. Representation of an image sequence (a) as a graph (b) of the 2D image structure.
Sometimes it is not necessary to keep a whole RAG, a spanning tree is enough. From all the spanning trees of a graph, the Minimum Spanning Tree [HK04] has the minimum sum of edge weights and characterizes the discrepancy of the represented image.
Integral features capture important properties of regions. The integral tree [KHP04] is a representation labeling each vertex of a tree with the integral feature(s) of the subtree.
Functional Graphical Models [MK03c] (FGM) describe dependence between variables by means of implicit equations. Explicit modeling of functional dependencies by a hypergraph, creates a structure well-adapted to information retrieval and processing.
The eccentricity transform [KIHF06] represents an image by assigning to each point the longest of the shortest paths to any other point of the image. It is robust against Salt & Pepper noise and articulated motion.
Data Structures
To represent the topology of a partition of the 2D plane, a pair of dual RAG+ can be used. Every edge in the primal graph is associated to an edge in the dual graph, and every vertex in the primal is associated to a face in the dual and vice versa.
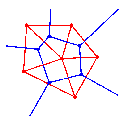
Combinatorial maps represent objects subdivided into cells of many dimensions. They use permutations (alpha, sigma) to encode relations between atomic elements called darts (half edges). In 2D, they act as planar graphs explicitly encoding the orientation of
edges around vertices (see Figure 2). Like combinatorial maps, generalized maps are defined in any dimension, and use only involutions.
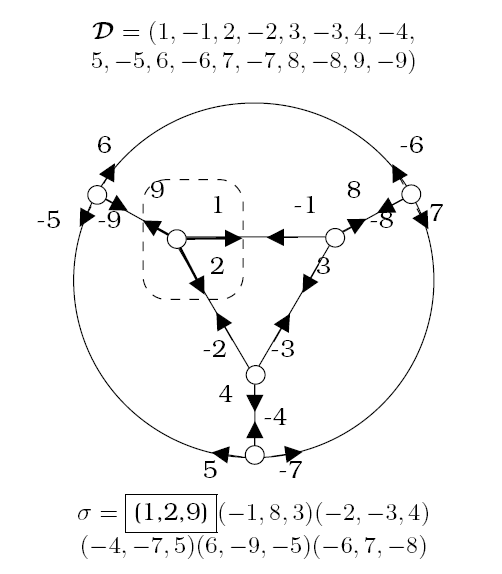
Figure 2. A combinatorial map defined by: set of darts and permutations sigma and alpha(d) = -d
Homology groups extend the Euler characteristic to a topological invariant that characterizes an object X by its "holes" in any dimension p=0..dim(X), (denoted p-holes). These holes can be seen as connected components in dimension 0, tunnels in dimension 1,
voids in dimension 2,... .
Operations on graphs
To reduce a graph or a map (e.g. when building a pyramid) contraction and removal operations are used. In 2D edge contraction removes the edge and identifies its end vertices. Edge contraction preserves the topology of the surviving elements. When building irregular pyramids, every contraction is followed by a simplification step, which removes redundant self loops and parallel edges i.e. empty self-loops and parallel edges bounding empty faces. Edges contracted in parallel form subtrees of the graph called contraction kernels [BK03a].
Where are Graphs Used?
Applications of graph based representations range from representations for cognitive vision [IHK05] inspired from human descriptions of videos [IHKH06], to graph-based fingerprint representation [OK04] encoding topology, to human problem solving and the Traveling Salesman Problem [PSS+06], to extraction of primitives (e.g. junction points, line segments) from graphs of digital points that are typically obtained from skeletonization [MK03b], to homotopic transformation for both combinatorial maps and weighted combinatorial maps [MKH03], and to efficient processing of huge amounts of structured sensory data for vision [Kro03].
References
| [BK02a] | L. Brun and W. G. Kropatsch. Defining regions within the combinatorial pyramid framework. In Computer Vision - CVWW’02, Computer Vision Winter Workshop, pages 198 – 207, Bad Aussee, Österreich, 2002. |
| [BK02b] | L. Brun and W. G. Kropatsch. Receptive fields within the combinatorial pyramid framework. In Discrete Geometry for Computer Imagery, 10th DGCI, pages 92 – 101, Bordeaux, Frankreich, 2002. |
| [BK03a] | L. Brun and W. G. Kropatsch. Contraction kernels and combinatorial maps. Pattern Recognition Letters, 24(8):1051 – 1057, 2003. |
| [BK03b] | L. Brun and W. G. Kropatsch. Construction of combinatorial pyramids. In 4th IAPR-TC15Workshop on Graph-based Representation in Pattern Recognition, pages 1 – 12, 2003. |
| [BK03c] | L. Brun and W. G. Kropatsch. Implicite encoding of combinatorial pyramids. In Computer Vision Winter Workshop 2003, page 6, 2003. |
| [BK05] | L. Brun and W. G. Kropatsch. Inside and outside within combinatorial pyramids. In M. vento L. Brun, editor, 5th IAPR-TC15 Workshop on Graph-based Representation in Pattern Recognition, pages 122 – 131, 2005. |
| [BK06] | L. Brun and W. G. Kropatsch. Contains and inside relationships within combinatorial pyramids. Pattern Recognition, 39(4):515 – 526, 2006. |
| [GPK02] | R. Glantz, M. Pelillo, and W. G. Kropatsch. Matching hierarchies of segmentations. In Computer Vision - CVWW’02, Computer Vision Winter Workshop, pages 149 – 158, Bad Aussee, ¨ Osterreich, 2002. |
| [GPK03] | R. Glantz, M. Pelillo, and W. G. Kropatsch. Hierarchical matching of panoramic images. In 12th International Conference on Image Analysis and Processing, pages 328–333, 2003. |
| [GPK04] | R. Glantz, M. Pellilo, and W. G. Kropatsch. Matching segmentation hierarchies. International Journal of Pattern Recognition and Artificial Intelligence, 18, 2004. |
| [HGS+02a] | Y. Haxhimusa, R. Glantz, M. Saib, G. Langs, and W. G. Kropatsch. Logarithmic tapering graph pyramid. In Proceedings of 24th DAGM Symposium, pages 117 – 124, Zürich, Schweiz, 2002. |
| [HGS+02b] | Y. Haxhimusa, R. Glantz, M. Saib, G. Langs, and W. G. Kropatsch. Reduction factors of image pyramid on undirected and directed graph. In Proceedings of the 7th. Computer Vision Winter Workshop, pages 29 – 38, Bad Aussee, 2002. |
| [HIK06a] | Y. Haxhimusa, A. Ion, and W. G. Kropatsch. Comparing hierarchies of segmentations: Humans, normalized cut, and minimum spanning tree. In Digital Imaging and Pattern Recognition, pages 95 – 103, Obergurgl, 2006. |
| [HIK06b] | Y. Haxhimusa, A. Ion, and W. G. Kropatsch. Evaluating hierarchical graphbased segmentation. In The 18th International Conference on Pattern Recognition, pages 195 – 198, Hong Kong, 2006. |
| [HIK06c] | Y. Haxhimusa, A. Ion, and W. G. Kropatsch. Irregular pyramid segmentations with stochastic graph decimation strategies. In Progress in Pattern Recognition, Image Analysis and Applications, pages 277 – 286, Cancun, Mexico, 2006. |
| [HIKB05] | Y. Haxhimusa, A. Ion, W. G. Kropatsch, and L. Brun. Hierarchical image partitioning using combinatorial maps. In D. Chetverikov, L. Czuni, and M. Vincze, editors, Hierarchical Image Partitioning using Combinatorial Maps, pages 179 – 186, 2005. |
| [HIKI05] | Y. Haxhimusa, A. Ion, W. G. Kropatsch, and T. Illetschko. Evaluating minimum spanning tree based segmentation algorithms. In A. Gagalowicz and W. Philips, editors, Computer Analysis of Images and Patterns: 11th International Conference, CAIP 2005, pages 579 – 586, 2005. |
| [HK03b] | Y. Haxhimusa and W. G. Kropatsch. Constructing stochastic pyramids by mides - maximal independent directed set. In 4th IAPR-TC 15 Workshop on Graph based Representation in Pattern Recognition, page 11, 2003. |
| [HK03c] | Y. Haxhimusa and W. G. Kropatsch. Hierarchical image partitioning with graph pyramids. In Proceedings of the 25th DAGM Symposium, page 8, 2003. |
| [HK03d] | Y. Haxhimusa and W. G. Kropatsch. Image partitioning with graph pyramids. In Proceedings of 25th AGM Workshop, page 7, 2003. |
| [HK04] | Y. Haxhimusa and W. G. Kropatsch. Segmentation graph hierarchies. In Proceedings of Joint International Workshops on Structural, Syntactic, and Statistical Pattern Recognition S+SSPR 2004, pages 343 – 351, 2004. |
| [HMK04] | A. Hanbury, J. Marchadier, and W. G. Kropatsch. The redundancy pyramid and its application to image segmentation. In Digital Imaging in Media and Education, Proc. of the 28th Workshop of the Austrian Association for Pattern Recognition (OAGM/AAPR), pages 157 – 164, 2004. |
| [IHK05] | A. Ion, Y. Haxhimusa, and W. G. Kropatsch. A graph-based concept for spatiotemporal information in cognitive vision. In M. vento L. Brun, editor, 5th IAPR-TC15 Workshop on Graph-based Representation in Pattern Recognition, pages 223 – 232, 2005. |
| [IHKB05] | A. Ion, Y. Haxhimusa, W. G. Kropatsch, and L. Brun. Hierarchical image partitioning using combinatorial maps. In H. Bischof A. Hanbury, editor, 10th Computer Vision Winter Workshop - CVWW 2005, pages 43 – 52, 2005. |
| [IHKH06] | A. Ion, H. Hausegger, W. G. Kropatsch, and Y. Haxhimusa. How humans describe short videos. In Proceedings of the Second International Cognitive Vision Workshop, 2006. |
| [IlHKH06a] | T. Illetschko, A. Ion, Y. Haxhimusa, and W. G. Kropatsch. Collapsing 3d combinatorial maps. In Digital Imaging and Pattern Recognition, pages 85 – 93, Obergurgl, 2006. |
| [IlHKH06b] | T. Illetschko, A. Ion, Y. Haxhimusa, and W. G. Kropatsch. Distinguishing the 3 primitive 3d-topological configurations: Simplex, hole, tunnel. In Proceedings of the 11th Computer Vision Winter Workshop, pages 22 – 27, Telc, Czech Republik, 2006. |
| [IKH06] | A. Ion, W. G. Kropatsch, and Y. Haxhimusa. Considerations regarding the minimum spanning tree pyramid segmentation method. In Structural, Syntactic, and Statistical Pattern Recognition, pages 182 – 190, Hong Kong, 2006. |
| [KH04a] | W. G. Kropatsch and Y. Haxhimusa. Grouping and segmentation in a hierarchy. In Computational Imaging II, pages 193 – 204, 2004. |
| [KH04b] | W. G. Kropatsch and Y. Haxhimusa. Hierarchical grouping of non-connected structures. In Digital Imaging in Media and Education, Proc. of the 28th Workshop of the Austrian Association for Pattern Recognition (OAGM/AAPR), pages 165 – 172, 2004. |
| [KH04c] | W. G. Kropatsch and Y. Haxhimusa. Hierarchies relating topology and geometry. In Cognitive Vision Systems, 2004. |
| [KH05] | W. G. Kropatsch and Y. Haxhimusa. Grouping of non-connected structures by an irregular graph pyramid. In P. Pina J. Marques, N. de la Blanca, editor, Pattern Recognition and Image Analysis: Second Iberian Conference, IbPRIA 2005, pages 107 – 114, 2005. |
| [KHL06] | W. G. Kropatsch, Y. Haxhimusa, and P. Lienhardt. Cognitive Vision Systems: Sampling the Spectrum of Approaches, chapter 13. Hiearchies relating Topology and Geometry, pages 199 – 220. Springer LNCS, Berlin - Heidelberg - New York, 2006. |
| [KHP04] | W. G. Kropatsch, Y. Haxhimusa, and Z. Pizlo. Integral trees: Subtree depth and diameter. In Proceedings of the IWCIA 2004, pages 77 – 87, 2004. |
| [KHPL05] | W. G. Kropatsch, Y. Haxhimusa, Z. Pizlo, and G. Langs. Vision pyramids that do not grow too high. Pattern Recognition Letters, 26(3):319 – 337, 2005. |
| [KIHF06] | W. G. Kropatsch, A. Ion, Y. Haxhimusa, and T. Flanitzer. The eccentricity transform (of a digital shape). In Discrete Geometry for Computer Imagery, pages 437 – 448, Szeged, Ungarn, 2006. |
| [Kro02] | W. G. Kropatsch. Abstraction pyramids on discrete representations. In Discrete Geometry for Computer Imagery, 10th DGCI, pages 1 – 21, Bordeaux, Frankreich, 2002. |
| [Kro03] | W. G. Kropatsch. Benchmarking graph matching algorithm. Pattern Recognition Letters, 24(8):1051 – 1059, 2003. |
| [KS02c] | W. G. Kropatsch and M. Saib. The optimal height of a graph pyramid. InVision with Non-Traditional Sensors 26th ¨ OAGM Workshop, pages 87 – 94, Graz, Österreich, 2002. |
| [LBK02] | G. Langs, H. Bischof, and W. G. Kropatsch. Hierarchical top-down enhancement of robust pca. In Proceedings of IAPR Int. Workshop on Syntactical and Structural Pattern Recognition (SSPR 2002), LNCS 2396, pages 131 – 136, Windsor, Kanada, 2002. |
| [MBK04] | J. Marchadier, L. Brun, and W. G. Kropatsch. Rooted kernels and labeled combinatorial pyramids. In Computer Vision Winter Workshop - CVWW’04, pages 59 – 68, 2004. |
| [MK03b] | J. Marchadier and W. G. Kropatsch. Extraction of curve segments and junctions by graph based optimization. In Vision in a Dynamic World 27th ÖAGM Workshop, 2003. |
| [MKH03] | J. Marchadier, W. G. Kropatsch, and A. Hanbury. Homotopic transformation of combinatorial maps. In Discrete Geometry for Computer Imagery, pages 134 – 143, Neapel, Italy, 2003. |
| [MKH04] | J. Marchadier, W. G. Kropatsch, and A. Hanbury. The redundancy pyramid and its application to segmentation on an image sequence. In DAGM Symposium 2004, pages 432 – 439, 2004. |
| [MK03c] | J. Marchadier and W. G. Kropatsch. Functional modeling of structures images. In 4th IAPR-TC15 Workshop on Graph-Based Representation in Pattern Recognition, page 12, 2003. |
| [OK04] | W. Ölz and W. G. Kropatsch. Graph representation of fingerprint topology. In Computer Vision Winter Workshop- CVWW’04, pages 51 – 58, 2004. |
| [PSS+06] | Z. Pizlo, E. Stefanov, J. Saalweachter, Y. Haxhimusa, and W. G. Kropatsch. Traveling salesman problem: A foveating pyramid model. The Journal of Problem Solving, 1(1):83 – 101, 2006. |
2014-2020 PRIP, Impressum / Datenschutzerklärung
This page is maintained by Webmaster ( webmaster(at)prip.tuwien.ac.at ) and was last modified on 20. May 2015 12:46